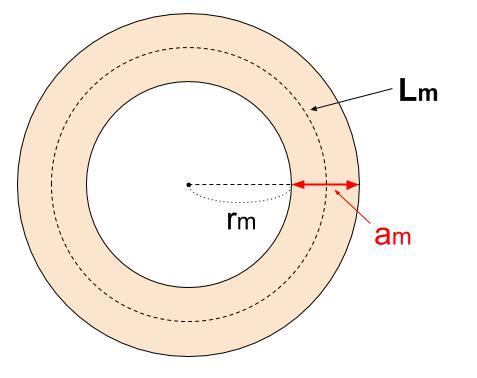
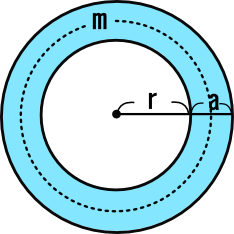
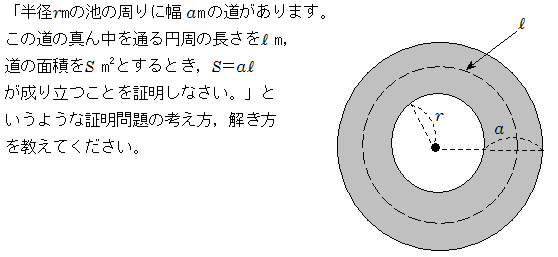
条件が比例式の等式証明 比の値、比例式という用語は中学で覚えたでしょうから省略します。 ⇒ 比例式および連比を利用して値を求める解き方 お決まりの方法を覚えてしまえば証明はそれほど難しくは 区分求積法の意味と例題と公式の証明 a ≤ x ≤ b a \leq x \leq b a ≤ x ≤ b において連続な関数 y = f ( x) y=f (x) y = f (x) に対して, lim n → ∞ b − a n ∑ k = 1 n f ( a ( b − a) k n) = ∫ a b f ( x) d x \lim_ {n \to \infty}\dfrac {ba} {n}\sum_ {k=1}^n f\left (a (ba)\dfrac {k} {n}\rightQ 中3の「式の活用(図形の証明)」についての問題です。 「半径rmの円形の土地の周りに、幅hmの道があります。 この道の面積をS平方メートル、道の中央を通る線の長さをlmとすると、S=lhとなることを証明しなさい。 」という問題です。 私はこの
中3第1章23式の計算の利用 整数の性質の証明 中学数学 1学期
式の利用 証明 ポイント
式の利用 証明 ポイント- 図形と方程式|座標を利用した証明について 今回は、座標を利用した証明について学習しましょう。 辺の長さの関係を表す等式が成り立つことを証明する際に、辺の長さを求めるのではなく、座標を用います。 座標を用いることで証明しやすくなるの不等式の証明の基本について 不等式 A > B を証明するには, A がだんだん小さくなるように変形していって,それでもなお B より大きいことを示せばよい. たとえば, √x4 2x2 2 > x2 1 を示すには (左辺) = √x4 2x2 2 > √x4 2x2 1 ← 根 号 の 中 の 値
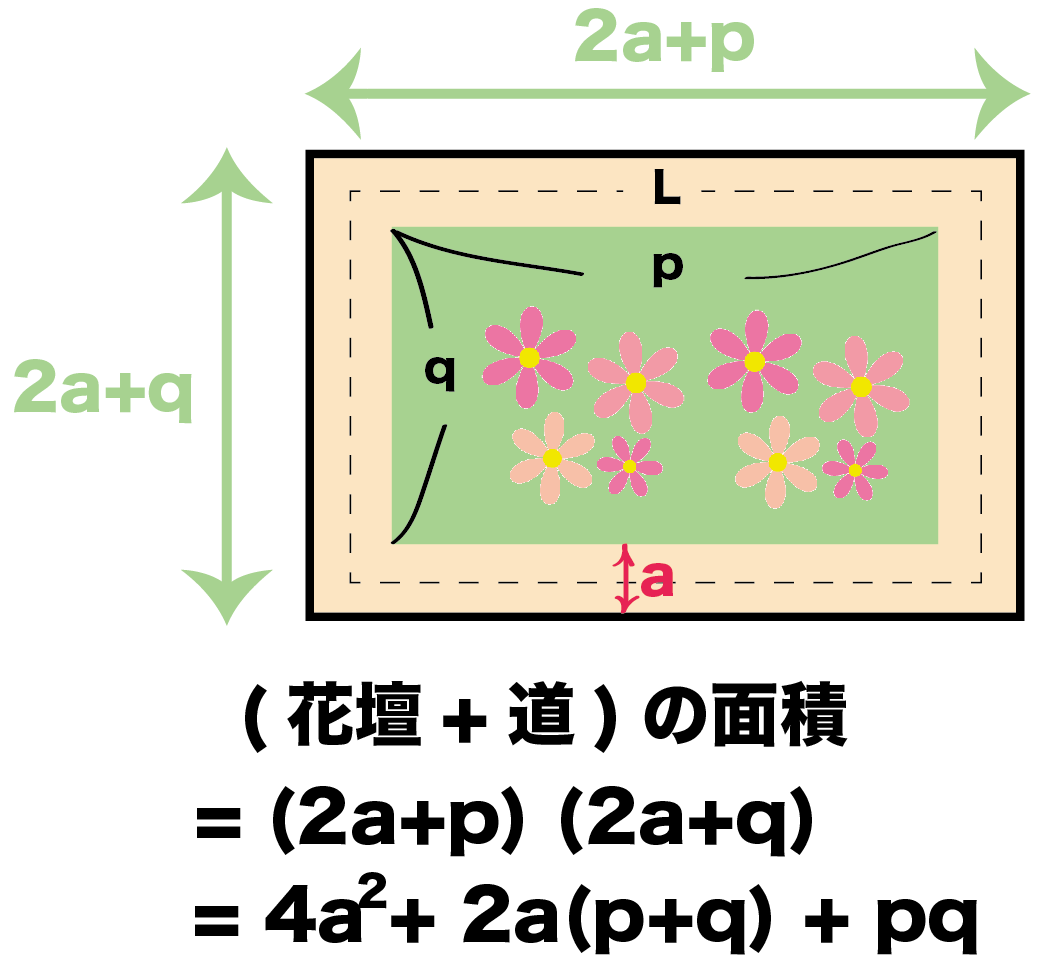



式の計算の利用 図形の証明問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
証明の書き方と、奇数や連続する整数の表しかたは中2の内容なので詳しくは触れない。 単に計算するときに展開や 因数分解 を使っているだけで、基本的な考え方は中2の時に学んだ書き方をそのままつかう。 一応少し復習しておく 1文字での表し方文字式の筆算のやり方を解説! 連立方程式 加減法の解き方をわかりやすく解説! 代入法の解き方を問題別に解説! 加減法、代入法の簡単な練習問題! 3つの文字、式の連立方程式を計算する方法;19/5/8 2年 式の計算総合問題1 2①と②の解答が逆になっていました。4の答が抜けておりました 2 3年2次方程式(因数分解利用)2⑥⑦, 類第1 2⑥, 類題2 2⑥符号間違い 1次関数総合問題Lv3 2②(5,9)(誤)→(5,9)(正)
♴ 式の計算の利用数や図形の性質を調べたり証明したりするために,式の計算が利用されることもある。 とくに,証明でよく使われる表し方には, 次のようなものがある。 ① 整数は n を使って表す。事例7 2年 式と計算「文字の式を使った証明」 (1)jsl生徒に対してこの課題を実施するねらい この課題では,2変数の文字の式の計算を利用して,2桁の自然数の性質について考 える。動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru
ごくまれに証明問題が大学入試で出題されるが,\ まあまあ難しい 数学的帰納法では通常n=kとして証明を行うが,\ Σk=0}{n}でkが使われているのでここではlを用いた 仮定した式を微分すると,\ f^{(nk)}g^{(k)}の部分が一致する組ができるので,\ それらを組み合わせるマチンの公式に類似した式は比較的探しやすいため、非常に多くの形の式が見つかっている。 この節では、その中のほんの一部を紹介する。 複素数を用いたマチンの公式の証明と同様の計算を用いるなどして、 計算機 を用いて公式を探索していくことも 文字式の利用の解き方がさっぱりわからん!? こんにちは!この記事をかいているKenだよ。うたたねが得意だね。 中2数学の「 文字式の利用 」はけっこうむずい。 ここでは、 文字式を利用して「すごいこと」をしなきゃいけないんだ。




数学2年 文字式の利用 塾の先生が作った本当に欲しいプリント 楽天ブログ




無料 中3数学 基本解説 解答プリント 307 式の計算7 式の計算の利用
19 2年 式の計算 文字式を利用した証明 1教材のねらい「文字の式」で扱った文字式による証明の有効性や簡嘩性を感得させたい0- 1 2 魅力的な誅超・扱い まず、課題1のように、具体的な数値を入れた問題を考えさせる。 課 趨 1「不思議な公式の証明!」 ~性質が成り立つ理由を式を使って説明する~ ☆本時のねらい:展開や因数分解を利用して図形の性質を証明することができる。 ☆本時の工夫点:①証明のかき方に慣れるために,教科書の証明を読み取り,理解する 時間を設定図2 3 ペル方程式では x, y の整数解を調べますが, D が平方数,例えば D=1 の場合 右図で赤で示したように漸近線が格子点( x, y とも整数となる点)を 無限個通る (*1)代わりに,双曲線は x 軸上の自明解( x=1, y=0 )以外には 格子点を1つも通りません (*2




式の計算の利用 図形の証明問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




世界一わかりやすい数学問題集中3 1章 式の展開と因数分解
また、三角不等式は 使い所を把握しておくことが大切 です。 三角不等式は 絶対値の和の結合や分解が式にあらわれている時 に利用することが多いです。 このことをよく覚えておいてください。 三角不等式を用いる証明問題の解き方 中3数学「数の証明」整数の利用を活用する!について記述しています。 レベル:標準 頻出度:定期テスト ポイント:証明の流れをつかむ数の証明のパターン主な出題パターンは、主に2つ。 倍数になることや割り切れることなど、「~に(なる)こ式の計算の利用① ・ くふう編 Lesson 2 式の計算の利用② ・ 代入編 Lesson 3 式の計算の利用③ ・ 数字の証明編 0009 Lesson 4



中学2年生の 文字式の利用 の問題です 問題右のカレンダー 下の写真 のよ Yahoo 知恵袋




世界一わかりやすい数学問題集中3 1章 式の展開と因数分解
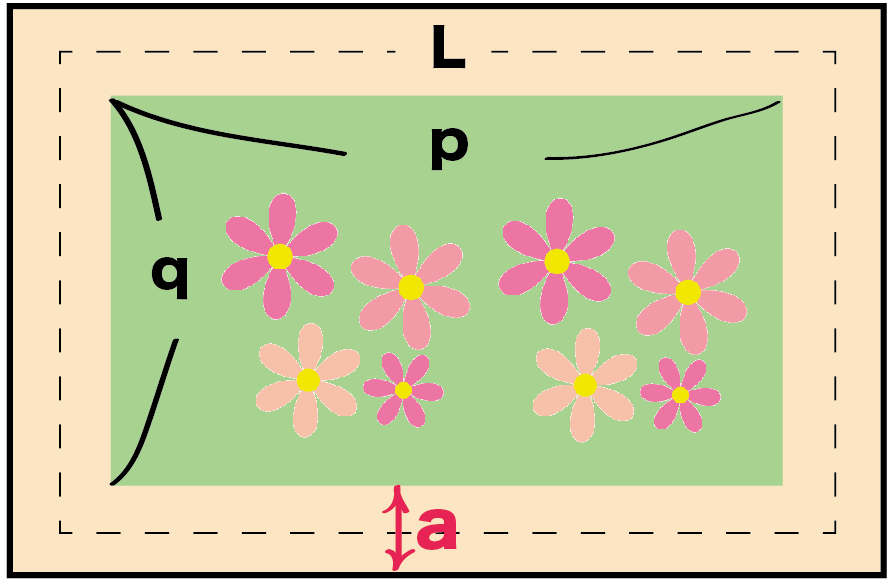
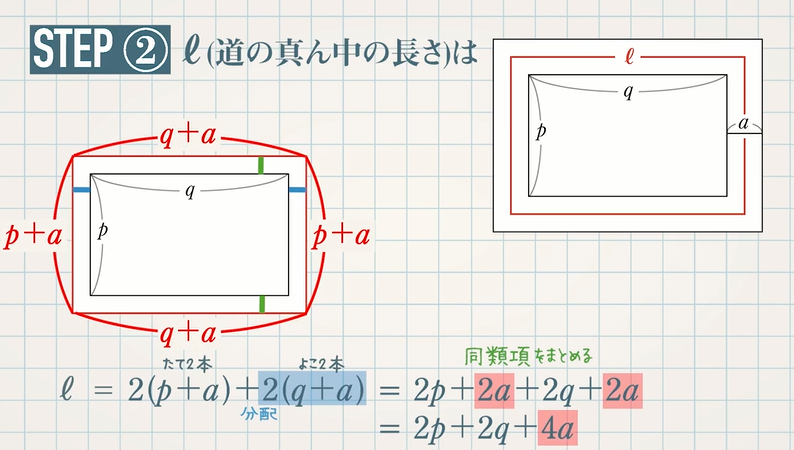
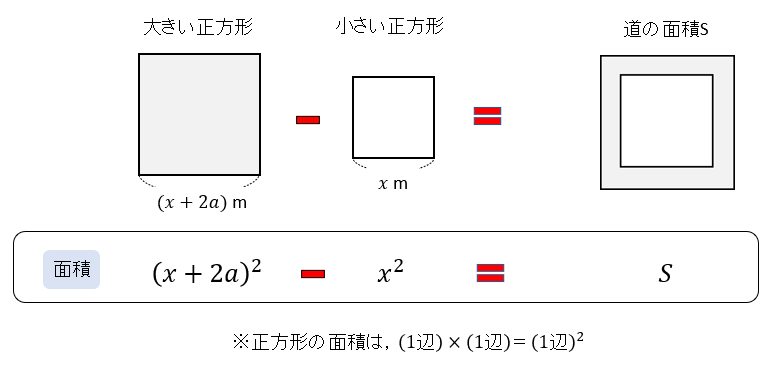
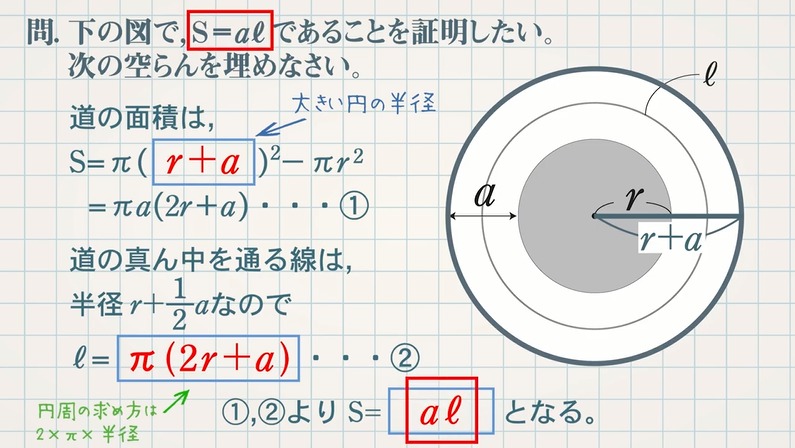
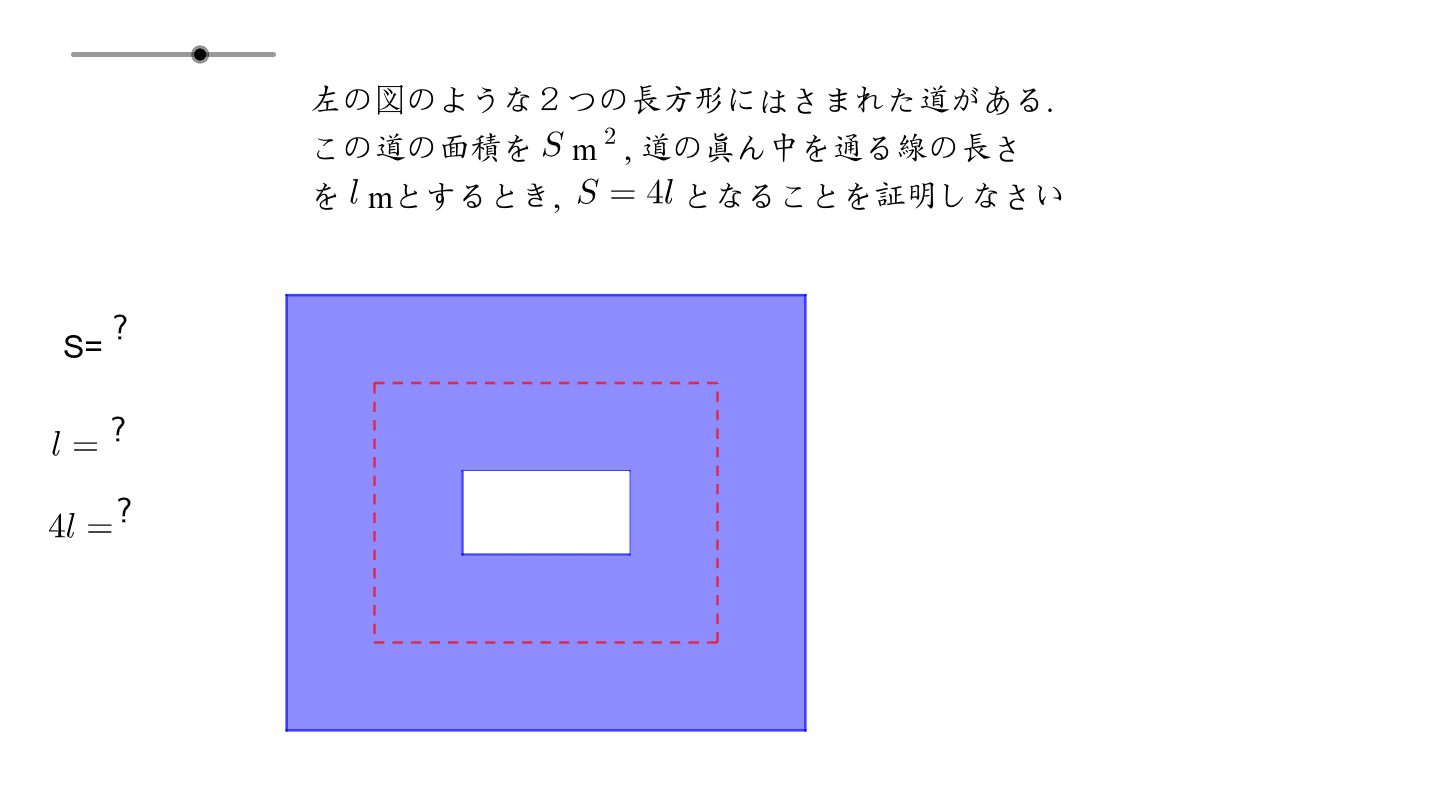
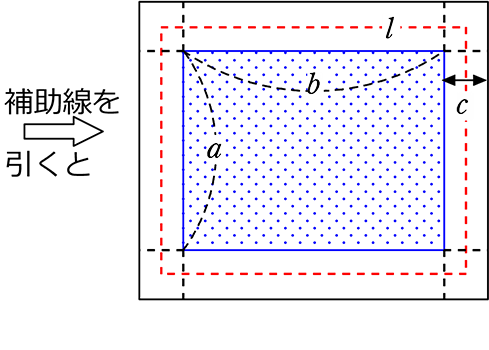
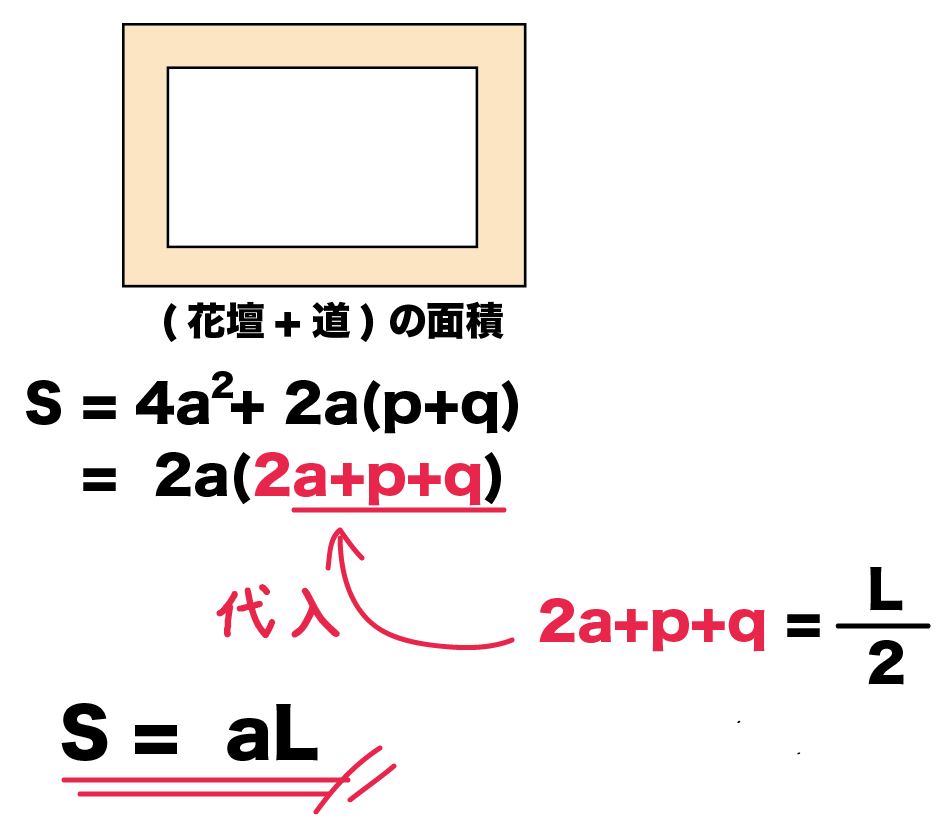
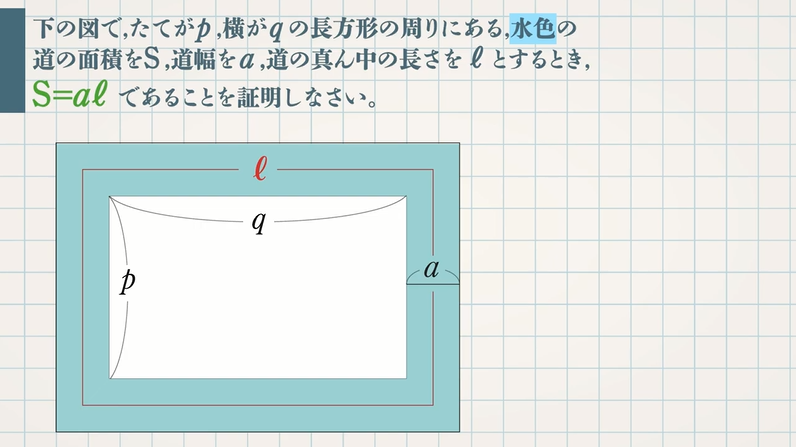
式の計算の利用 解説 x 2 2xa を因数分解すると、(x3)(xm) になるという。mとaの値を求めなさい 次のことがらを証明しなさい。${\rm S}=aℓ$ の証明は次の $3$ つのSTEPで解くので、しっかり流れを確認しましょう。 STEP①:大きい方の図形から小さい方の図形を引いて、 $\textcolor{blue}{{\rm S}}$ (道の面積)を $\textcolor{blue}{a,p,q}$ を用いた式で表す STEP②: $\textcolor{blue}{ℓ}$ (道の真ん中の長さ)を $\textcolor{blue}{a,p,q}$ を用いた① 不等式 の証明では、 (大きい値-小さい値)を計算して であることを示します。 ② 平方を完成させて、その部分が 0 以上であることを使って証明します。 ③ 解答の最初に、これから証明しようとする不等式「 」を書く必要はありません。 書くときは解答例で示したように式の後に「を




保存版 2項係数の関係式の証明 応用編 恒等式の利用 Sacramy




展開 因数分解の利用 式の証明 清水塾
編集スタッフ01 中2数学文字式の利用とは? 「文字を使った説明」の仕方を解説! こんにちは、あすなろスタッフのカワイです! 式と計算という単元では、単項式や多項式といった文字式についての計算を学んできたと思います。 今回はその では例題の立式をしてみましょう。 連続する二つの奇数の和が4の倍数になることを証明しなければなりません。 そして立式するために「連続する二つの奇数」という言葉は「2n1 , 2n3」という文字式で表してあります。中学校2年文字式の利用3/6時間・式の計算12/16時間(東京書籍新しい数学2 p22) 思考の開始 Aさんの メモがき→ ・5の倍数になります。 ・真ん中の数の5倍になります。




中3数学 式の計算の利用 数に関する証明 まとめと問題




中学3年数学練習問題 式の利用 証明 式の展開 因数分解の応用
を使った式で表せ。 (2) yこの正の整数の十の位の数と一の位の数を入れかえてできる2 けたの正の数を,x, を 使った式で表せ。ただし,もとの数の一の位は0 ではないものとする。 解答欄 (1) (2)多項式・因数分解の利用(2)証明問題 ~中学3年生の数学~ このページは『多項式・式の計算の利用』‥一般的に言う応用問題の中の証明問題 (文章問題)の解説になります。 証明には型のような手順がありますので覚えていってくださいね! 1 多項式式の計算の利用①(証明) 名前 /4点 奇数の2乗が奇数になることを証明します。(���)の中にあてはまる数や式を答えなさい。<証明>



50 中3 数学 式の計算の利用 証明 問題 ニスヌーピー 壁紙




式の計算の利用 さわってうごく数学 Aquaアクア For Android Apk Download
高校数学Ⅱ 式と証明 当カテゴリでは式と証明分野のパターンを網羅する。 一部のパターンはかなりハイレベルで他分野の知識を要するために初学者には難しいが、それ以外はかなり基本的なパターンばかりである。 この分野の問題は、大学入試において文字式を利用した証明の練習です。 2年生になると、証明問題が入ってきます。 中間テストでは、 下例のような2けたの整数の入れかえ問題 奇数と偶数の問題 連続する整数の問題 カレンダーの問題 倍数を見分ける問題 などが 出題されます。




式の計算の利用と練習問題 基 数学の解説と練習問題



ベスト 中3 数学 因数分解 証明 問題 中3 数学 因数分解 証明 問題




式の計算の利用と練習問題 基 数学の解説と練習問題




中3 中3数学 式の計算の利用 中学生 数学のノート Clear
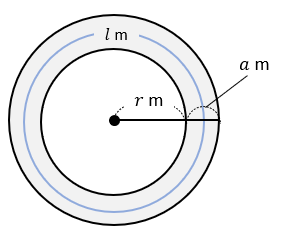



中3 式の計算の利用 円 正方形の図形の証明をイチから 数スタ



1
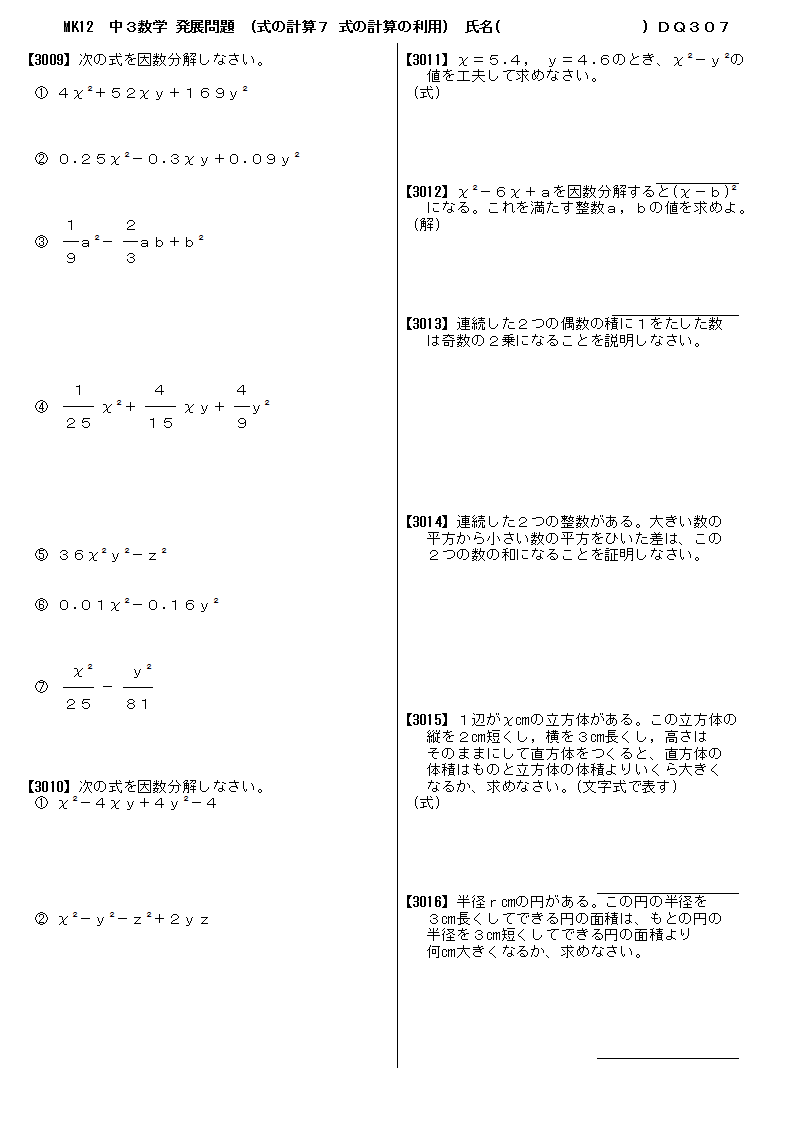



無料 中3数学 発展 応用問題 問題プリント 307 式の計算7 式の計算の利用




数学ia 三角形に関する等式の証明 大学入試数学の考え方と解法




中学3年 数学 式の計算の利用 2学期中間テスト 証明問題と解答 赤城 ᐡᐤᐡ




中3 展開 因数分解 S Aℓの証明 式の計算の利用 図形編 Youtube



式の計算の利用 図形の証明問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく



式の計算の利用




数学 中3 14 式の計算の利用 図の証明編 Youtube




合同式の問題の解き方 合同式の性質の証明 高校生向け受験応援メディア 受験のミカタ



中2数学 無料youtube授業一覧 動画 プリント 19ch




中3数学 式の計算の利用 数に関する証明 まとめと問題



Http Tyu Oita Ed Jp Hita Mikuma E5 8d 98 E5 85 E8 A8 E7 94 Ef E7 Ac Ac Ef 93 E5 Ad A6 E5 B9 B4 80 80 Ef 91 E7 Ab A0 Ef 9a E5 8f 81 Ae E8 A8 E7 Ae 97 81 Ae E5 E7 94 A8 Ef Pdf




式の計算の利用 02 証明への利用 図形問題への利用 中3数学 その9 Youtube




中学3年の数学 動画 式の計算の利用 図の証明編の問題 19ch



S Aℓの証明 式の計算の利用 図形編 教遊者




式の証明 清水塾



中3 式の計算の利用 円 正方形の図形の証明をイチから 数スタ



1



中学数学 式の展開 因数分解



S Aℓの証明 式の計算の利用 図形編 教遊者



中3第1章23式の計算の利用 整数の性質の証明 中学数学 1学期



中学数学 式による説明 図形 中学数学の無料オンライン学習サイトchu Su




式の計算の利用 図形の証明問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




式の計算 式による図形の証明問題の解き方のコツ 中学数学 定期テスト対策サイト




中3数学 式の利用 整数の証明問題の定期テスト対策予想問題 Atstudier




高校数学 二項係数ncrの和の等式 二項定理の利用 受験の月



Www Zkai Co Jp Wp Content Uploads 06 6b7c023db5d0e1e9d0beb391 Pdf



2




中3 中3数学 式の計算の利用 中学生 数学のノート Clear




式の計算の利用と練習問題 基 数学の解説と練習問題



式の計算の利用 図形の証明 Geogebra




中3 中3 式の計算の利用 証明問題 中学生 数学のノート Clear



Hd限定中3 数学 式の計算の利用 最高のカラーリングのアイデア




中学2年生 数学 文字式の活用 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




解説動画 中3数学 式の計算の利用




中3 中3数学 式の計算の利用 中学生 数学のノート Clear



中学3年数学練習問題 式の利用 証明 式の展開 因数分解の応用



式の計算の利用 図形の証明問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




中学2年生 数学 文字式の活用 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




展開 因数分解を利用する問題 鶴城数人 Note



Q Tbn And9gcsmd Q Fdzwkmorwtu6dtz1mvtxq0gtsuuqz8gxkja1c5dn1zlq Usqp Cau



式の計算 式による図形の証明問題の解き方のコツ 中学数学 定期テスト対策サイト



S Aℓの証明 式の計算の利用 図形編 教遊者




中3 展開と因数分解22 式の計算の利用4 中学数学の勉強に



中3 式の計算の利用 円 正方形の図形の証明をイチから 数スタ



中学校の数学の文章問題 文字式の応用問題



Www Kyo Kai Co Jp Img Material Chuu 1691 Sc S3 Mokuji Pdf




式による証明 無料で使える中学学習プリント



3 24第1章式の計算の利用 図形の性質の証明 中学生



1



3 23第1章式の計算の利用 整数の性質の証明 中学生




教科書レベルの問題一覧と解答 数学 式と証明 教科書より詳しい高校数学



Math 式の計算の応用 図形と証明 働きアリ
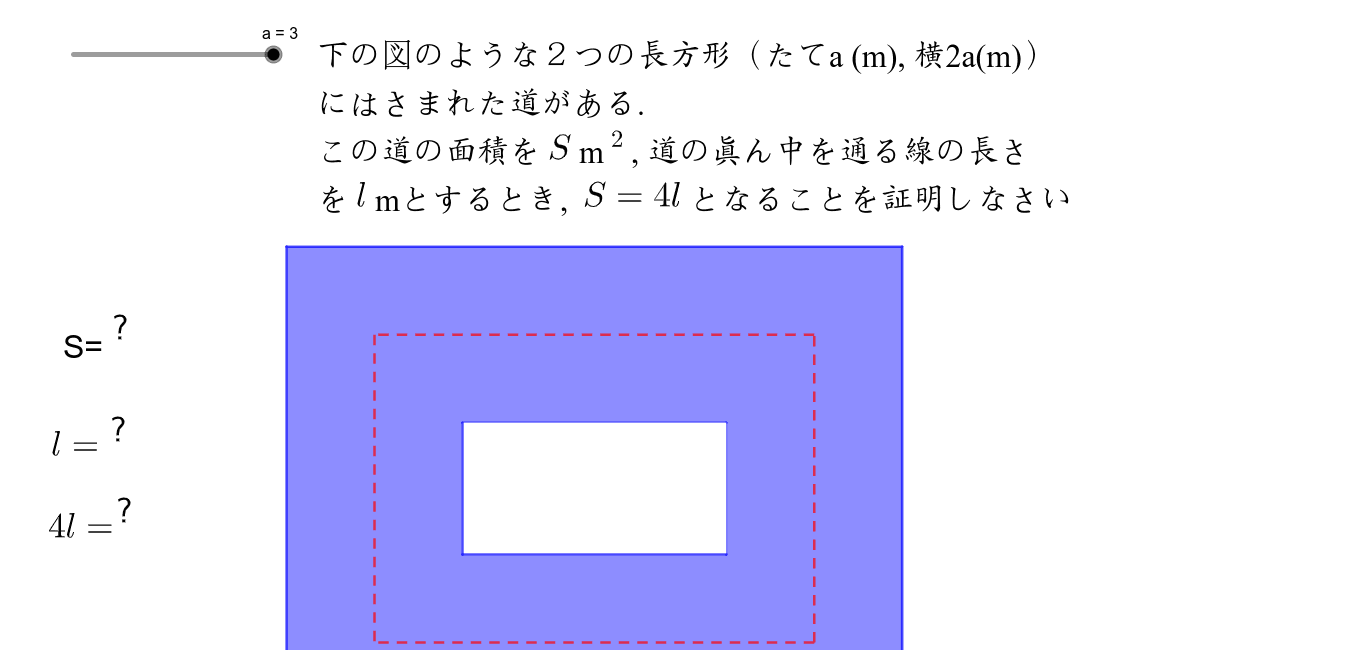



式の計算の利用 図形の証明2 Geogebra




式による証明 無料で使える中学学習プリント




中3 式の計算の利用 円 正方形の図形の証明をイチから 数スタ




数学 中学3年 式の計算の利用 ニコニコ動画




中学数学 式による説明 のコツと練習問題



因数分解でやる 図形の証明がわかりません 正方形や長方形はできたのですが 長方 Yahoo 知恵袋




中3 展開と因数分解22 式の計算の利用4 中学数学の勉強に




大注目 中学2年生数学dvd全10枚 Dvd教材サントップ店 Subaruqatar Com
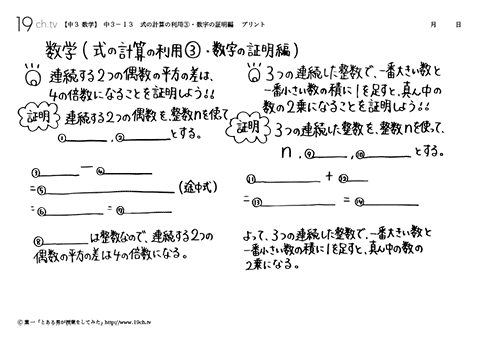



中学3年の数学 動画 式の計算の利用 数字の証明編の問題 19ch




メルカリ 中学数学 計算 3年 式の計算の利用 参考書 444 中古や未使用のフリマ




中学数学 式による説明 図形 中学数学の無料オンライン学習サイトchu Su




中学数学 式による説明 のコツと練習問題




たけのこ塾 中2数学 今回は 文字式の利用 の証明問題を作成しました 今回のポイントは次の2つです 2ケタの整数を 2つの文字を使って表す方法 ある数 の倍数は 整数 で表される 詳しくは画像の解説をご覧下さい 勉強垢 中2




たけのこ塾 中2数学 今回は 文字式の利用 の証明問題を作成しました 今回のポイントは次の2つです Facebook



中学三年生の式の展開と因数分解の利用の図形の性質の証明の仕方 Yahoo 知恵袋




展開 因数分解の利用 証明 無料で使える中学学習プリント




式による証明 無料で使える中学学習プリント




P 21 Lihat Cara Penyelesaian Di Qanda




中3数学 式の計算の利用 1学期期末テスト 赤城 ᐡᐤᐡ




文字式の利用 証明 文字について解く 中学生 数学のノート Clear



中学校3年生の数学の授業




中3数学 式の計算の利用 1学期期末テスト 赤城 ᐡᐤᐡ




式の計算の利用 図形の証明問題の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
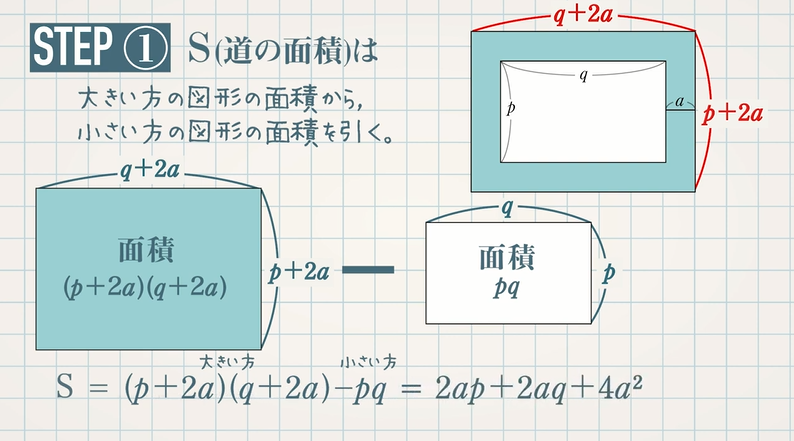



S Aℓの証明 式の計算の利用 図形編 教遊者




数学 中3 13 式の計算の利用 数字の証明編 Youtube




中3 中3数学 式の計算の利用 中学生 数学のノート Clear




高校数学 ド モアブルの定理による3倍角の公式 三角関数の等式の証明 受験の月




中3 数学 式の計算の利用 1学期期末テスト 赤城 ᐡᐤᐡ




Hd限定中3 数学 式の計算の利用 最高のカラーリングのアイデア
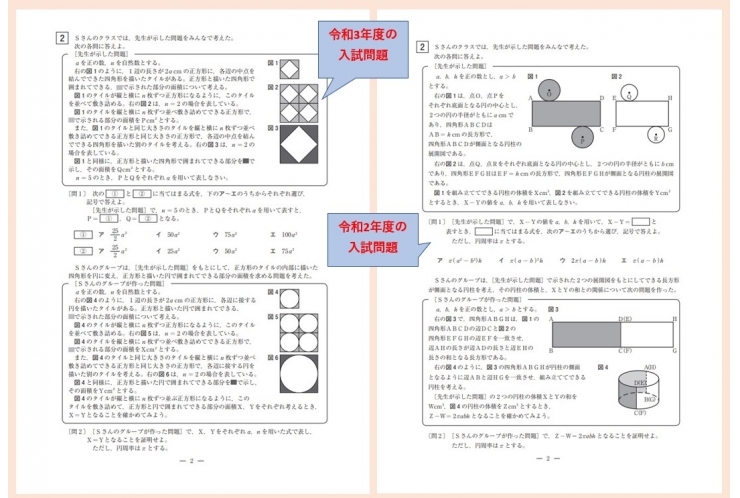



文字式の利用 演習してますか 勉強方法




中3 中3 数学 式の利用 中学生 数学のノート Clear




数学 中2 9 文字式の利用 基本編 Youtube




中学3年数学 式の展開と因数分解 式の計算の利用 2確認問題1 あんのん塾




中学数学 式の展開 因数分解



0 件のコメント:
コメントを投稿